April 14th, 2024
Unlocking the Secrets of the Mann-Whitney U Test
By Alex Kuo · 7 min read

Overview
In the vast realm of statistical tests, the Mann-Whitney U test stands out as a robust non-parametric alternative to the independent sample t-test. But what does "non-parametric" mean? And when should you use the Mann-Whitney U test? Let's dive deep into this statistical tool and unravel its intricacies.
What is the Mann-Whitney U Test?
Assumptions Behind the Test
1. Random Sampling: The samples drawn from the population must be random.
2. Independence: Observations within each sample must be independent of each other. Additionally, an observation can belong to only one group, not both.
3. Ordinal Scale: The data should be on an ordinal measurement scale.
Calculating the Mann-Whitney U
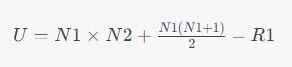
U = Mann-Whitney U test statistic
N1 = Sample size of the first group
N2 = Sample size of the second group
R1 = Rank sum of the first group
Applications of the Mann-Whitney U Test
- Psychology: To compare attitudes, behaviors, or perceptions.
- Medicine: To evaluate the efficacy of two different medications or treatments.
- Business: To gauge consumer preferences or assess regional variations in product popularity.
Questions Suited for the Mann-Whitney U Test
- How do horse racing outcomes vary between male and female horses?
- Do university preferences differ based on the geographic region of students, such as urban vs. rural?
Interpreting the Results
One of the challenges with the Mann-Whitney U test is its interpretation. Instead of presenting results in group mean differences, as many are accustomed to, it showcases group rank differences. This shift in presentation can be a tad confusing, but tools like Julius.ai can help translate these results into plain English, making them more digestible.
Conclusion: Harnessing the Power of Julius
Understanding and implementing the Mann-Whitney U test can be daunting, especially when interpreting its results. This is where Julius.ai steps in. With its advanced analytical capabilities, Julius can assist in performing the Mann-Whitney U test, ensuring accurate results and clear interpretations. Whether you're a researcher, student, or professional, Julius is here to simplify your statistical journey.
